ソルバ機能
動力学解析手法の概説
Lagrancia Dynamicsでは、MBSの運動を表すシステムの状態方程式をルンゲクッタ法などで数値的に解くことで、ある時刻における位置・速度・加速度を解析します。 \begin{eqnarray*} \dot{\bm{y}}=\bm{F}(\bm{y},t) =\left[ \begin{array}{c} {\dot{\bm{q}}} \\ \ddot{\bm{q}} \\ \end{array} \right]\,\, \small{\cdots\,システムの状態方程式}\\ \end{eqnarray*} \begin{eqnarray*} \small \begin{array}{ll} \bm{q}:一般化座標,\;\dot{\bm{q}}:一般化速度,\;\ddot{\bm{q}}:一般化加速度 \end{array} \normalsize \end{eqnarray*} この状態方程式を解くために必要な初期条件(初期一般化座標$\bm{q}_0$と初期一般化速度$\dot{\bm{q}}_0$)は、設定値として与えます。 未知の変数である一般化加速度については、運動方程式と加速度レベルの拘束方程式から成る連立方程式を解くことで得ます。(拡大法)
動力学解析の実行
解析を行うには、コントロールバーの「動力学解析ボタン」をクリックし、動力学解析ダイアログを表示します。

動力学解析ダイアログで、解析に必要な情報を入力後、解析開始ボタンをクリックすることで解析処理が開始されます。
動力学解析ダイアログ
【一般タブ】
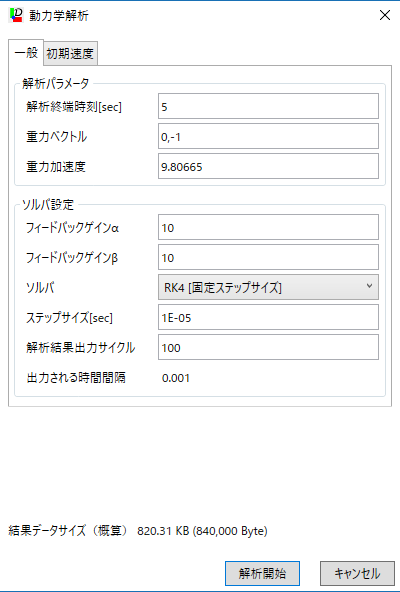
- 解析終端時刻
- 解析の範囲を指定します。0秒時点から解析終端時刻までに関して解析を行います。
- 重力情報(重力ベクトル,重力加速度)
- 重力ベクトルは、重力の向き[x,y]を絶対座標系(画面水平方向右向きを正とするX軸-垂直方向上向きを正とするY軸)で表現します。 解析時には、正規化された重力ベクトルに重力加速度を乗じて重力情報とします。
- フィードバックゲインα,フィードバックゲインβ
- 拘束方程式の数値計算で生じる誤差の拡大を抑制するために、解析にはフィードバック制御が組み込まれています(バウムガルテの安定化法)。 フィードバックゲインα,フィードバックゲインβはその調整値です。通常はα=β=1〜50程度の値が用いられます。
- ソルバ
-
システムの状態方程式(常微分方程式)を解くために使用する解析器を選択します。
- RK4[固定ステップサイズ]
- Runge-Kutta法4次公式を使用して、固定ステップサイズでシステムの状態方程式を数値的に解きます。
- RKF45[可変ステップサイズ]
- Runge-Kutta-Fehlberg法を使用して、ステップサイズを自動調節しながらシステムの状態方程式を数値的に解きます。
- RKDP5[可変ステップサイズ]
- Dormand–Prince法を使用して、ステップサイズを自動調節しながらシステムの状態方程式を数値的に解きます。
以下の項目は、ソルバに固定ステップサイズ型(RKF4)が選択された場合のみ表示されます。
- ステップサイズ
- 単位は秒です。
- 結果出力サイクル
- 解析結果の出力頻度を調整します。ここで指定したサイクルで出力します。
- 出力される時間間隔
- 出力される解析結果データの時間刻み幅を表します。これは解析間隔×結果出力サイクルから算出されます。 図の例の場合、解析結果(各ボディの位置・速度・加速度の情報)が0.001秒間隔で出力されます。
以下の項目は、ソルバに可変ステップサイズ型(RKF45,RKDP5)が選択された場合のみ表示されます。
- 初期ステップサイズ
- 解析開始時のステップサイズ。単位は秒です。
- 最大ステップサイズ
- 自動的に変動するステップサイズが取りうる最大値。単位は秒です。
- 接触時ステップサイズ係数
-
Lagrancia Dynamicsでは"接触条件"が定義されている2つのボディが接触しそうになると、
解析ステップサイズを”接触時ステップサイズ”に収束させる制御が実装されています。
この制御は可変ステップサイズ型ソルバが持つ「ステップサイズの自動調節機能」よりも優先されます。
”接触時ステップサイズ”は、最大ステップサイズに接触時ステップサイズ係数を乗じた値が使用されます。
0より大きく1以下の値を入力してください。 - 絶対許容誤差,相対許容誤差
- 可変ステップサイズ型ソルバではステップサイズを自動的に調節しながら解析時刻を前に進めます。
システムの状態方程式(常微分方程式)をテイラー展開したときの、
4次の項までの近似値と5次の項までの近似値の差が0に収束するようにステップサイズを調節します。
絶対許容誤差と相対許容誤差はこの際の4次近似値と5次近似値との誤差評価の際に使われます。
接触条件で動摩擦係数を設定している場合、この収束計算と相性が悪いために解析時間が長くなる傾向があります。 - 結果出力間隔
- 単位は秒です。
結果出力間隔内で最初の解析時ステップの計算結果を当該間隔の結果として出力します。
出力される処理結果の"解析時刻"の項は解析時の時刻です。
例外として、初回0と最終時刻は、その時刻を解析時ステップとして、必ず出力します。
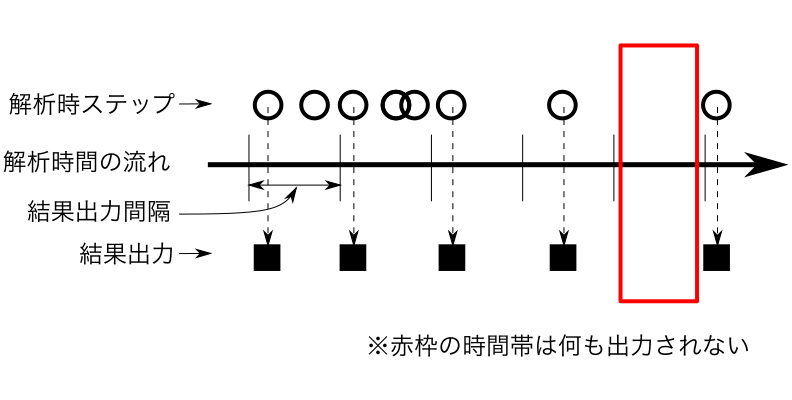
解析ステップと結果出力間隔の関係
【初期速度タブ】
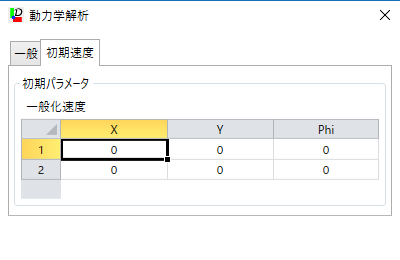
- 一般化速度x,y,Phi
- 解析開始時刻(0秒)時点での全ボディの一般化速度情報を表形式で表示します。
番号1〜は、アウトライナー上でのボディの並び順と一致します。
Xおよび、Yの単位は$\mathrm{m/sec}$です。Phiの単位は、$\mathrm{rad/sec}$です。
この画面では、解析時の各ボディの初期速度情報を一時的に変更できます。ここで変更した内容は保存されません。